Introdução
Quando olhamos uma imagem temos a tendência de procurar padrões o que reduz o esforço e tempo necessário para identificar do que se trata. Em análise de dados filtros podem ser aplicados com a mesma motivação.
Enquanto o processo de filtragem em um conjunto de pontos é apresentado em cursos acadêmicos e tutoriais, existe pouco material em relação a grafos. Portanto, criei esse post para discutir o conceito de filtragem e padrões em grafos e as diferentes maneiras de se obter tal filtragem. Tentei ser didático o suficiente para que uma pessoa fora da computação ou exatas (que esteja iniciando em dados) consiga compreender o texto. Sinta-se à vontade para pular qualquer seção do post :)
Os exemplos desse post usam python e as seguintes bibliotecas:
$ python3 -m pip install numpy matplotlib networkx
Lista de Conteúdos
O que é um grafo?
Um grafo é uma estrutura de dados que você constantemente está em contato. Alguns exemplos: sua rede de seguidores e seguidores no twitter, as transações financeiras associadas a sua chave PIX, as relações de repositório e contribuições no github, etc.
Um grafo armazena objetos que têm relações pares a pares entre si. Sendo que é possível associar a cada objeto ou relação um outro tipo de dado genérico tais como um número real, um vetor, uma imagem ou mesmo outro grafo.
A imagem abaixo representa um grafo dirigido formado por 4 vértices.
graph TD;
A-->B;
B-->A;
A-->C;
B-->D;
C-->D;
Vamos usar a letra $G$ para representar um grafo. A letra $V$ para o conjunto de vértices (objetos) e $E$ para o conjunto de arestas (relações). Na imagem acima nosso grafo seria dado então pelo conjunto $V=\{A,B,C,D\}$ e $E=\{(A,B), (B,A), (A,C), (B,D), (C,D)\}$.
Como disse no início desta seção é possível associar coisas tanto as arestas quanto os vértices. Por exemplo, o grafo abaixo poderia representar transações financeiras entre 3 pessoas e o valor que cada uma tem em sua conta corrente
graph TD; A[A R$100,00]-->|R$1|B; B[B R$3,00]-->|R$2|A; C[C R$0]-->|R$0,50|A;
Tais grafos de transações financeiras são usados, por exemplo, para detectar crimes de lavagem de dinheiro, formação de quadrilhas e fraudes quando o comportamento de um dado cliente é anómalo. Os valores nas arestas são os pesos do grafo.
O que é filtragem?
Filtro tem origem na palavra feltro. O feltro era o material feito principalmente de lã usado antigamente para separar um líquido de suas impurezas. Um filtro em análise de dados é a mesma coisa: uma ferramenta que separa um conjunto de dados de uma sujeira, ruído. Portanto, assim como para filtrar uma bebida temos que decidir antes algumas coisas:
- O que queremos que seja removido?
- O quão eficiente é nosso filtro?
- Qual é o resultado esperado?
Filtragem para remover ruídos
Talvez a primeira coisa que vem à sua cabeça quando ouve a palavra filtro é Instagram. Alguns filtros de fotos feitos para embelezar nada mais são que um filtro para remoção de ruídos.

O que consideramos ruído depende das respostas das perguntas que levantei anteriormente. Um ruído em uma imagem pode ser uma contribuição espúria devido ao sensor de uma câmera ser ruim. Um ruído pode ser também algo intrínseco, por exemplo os poros e rugas na sua pele.
Filtragem para ressaltar características e Gestalt
Os princípios de Gestalt são suposições de certas leis sobre como a mente humana processa imagens através do reconhecimento de padrões. Em resumo, tal princípio estabelece que a percepção não é baseada em elementos individuais, mas em padrões em que os elementos são arranjados ou têm contrastes entre si. Você não compreende uma imagem analisando cada pixel individualmente, mas como os pixels se organizam e diferem entre si!
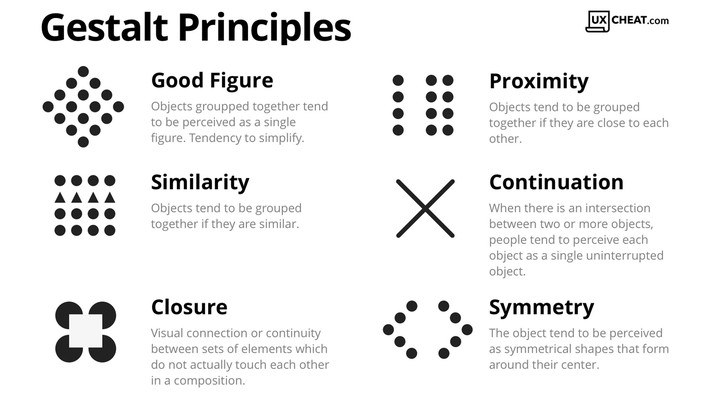
Como se relaciona com os grafos? Um dos porquês para realizar a filtragem de um grafo consiste em remover relações (arestas) espúrias para ressaltar um dado padrão que queremos analisar. Comumente, esse padrão são estruturas de comunidades e/ou agrupamentos obtidos via métodos de visualização.
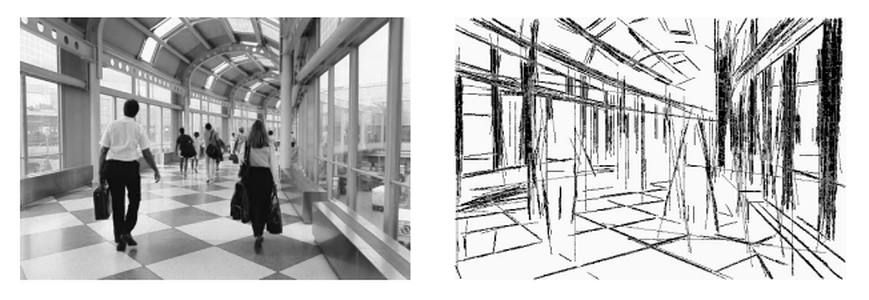
Na imagem acima é mostrado o resultado de um método baseado na Gestalt para simplificar uma imagem. Em que um algoritmo extrair um padrão de linhas de uma imagem. Em redes complexas temos o conceito de backbones que são uma espécie de espinha dorsal, esqueleto, que representa as relações mais importantes entres os vértices (ficará mais claro na seção sobre backbones . Nesse ponto não necessariamente estamos removendo relações assumindo que elas são um ruído da nossa medida, mas apenas queremos ressaltar esse backbone.
Filtragem para reduzir o custo computacional
Embora a filtragem possa ser usada para remover uma contaminação em um dado e/ou facilitar termos insights Conseguimos também reduzir o custo computacional de algoritmos que atuam nesses dados. Um exemplo simples é mostrado no código abaixo:
import numpy as np
import io
X, Y = np.meshgrid(
np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
z = np.exp(-0.1*(X**2 + Y**2))
z_noise = z + np.random.normal(0, 0.1, z.shape)
z = (z / z.max()*255).astype(np.uint8)
z_noise = (z_noise / z_noise.max()*255).astype(np.uint8)
data_noisy = io.BytesIO()
data = io.BytesIO()
np.savez_compressed(data_noisy, z_noise)
np.savez_compressed(data, z)
print(f"Noisy {data_noisy.getbuffer().nbytes/10**6:.1f} MB")
print(f"Original {data.getbuffer().nbytes/10**6:.1f} MB")
Noisy 3.6 MB
Original 0.2 MB
O output indica que o resultado de contaminação por ruído aumenta o custo de armazenamento de um mesmo padrão de dados.
Em grafos, filtrar para reduzir custo computacional costuma ser essencial. Por exemplo, muitos algoritmos escalam com o número de arestas. Portanto, um grafo em que cada par de vértices tem uma aresta teria custo computacional $O(número\ \ de\ \ vértices^2)$ o que é impraticável para apenas algumas dezenas de milhares de vértices. Portanto, tornando a análise de dados impossível.
Confusões sobre o que é filtragem em grafos
Antes de entrar mais a fundo na filtragem de grafos é melhor você ler com calma a seguinte desambiguação para você não ficar perdido na literatura.
Desambiguação.
A área de grafos/redes foi/é é meio bagunçada pois cada campo de estudos (engenharia, computação, matemática, física, sociologia, etc) costuma reinventar o mesmo método com outro nome ou usar nomes iguais para coisas diferentes.
-
Graph coarsening
Em ciência da computação: o processo de obter uma representação mais grosseira de um grafo removendo arestas e/ou vértices.
-
Edge filtering:
Em ciência da computação: o processo de aplicar um filtro (processamento de sinais) em valores definidos nas arestas. Uma filtragem nos valores associados às arestas!
Outras disciplinas: o processo de remover arestas que não se adequam a um dado padrão.
-
Graph sparsification
Termo usado para representar tanto a remoção de vértices quanto arestas (no mesmo sentido de graph coarsening). Por exemplo: “spectral edge sparsification”. Contudo, é mais utilizado quando você parte de um grafo vazio (sem relações) e vai adicionando tentando preservar as propriedades espectrais do grafo original.
Você pode encontrar trabalhos com o termo spectral filtering ou spectral coarsening , ambos significando a mesma coisa. Contudo, spectral filters costuma ser usado mais em trabalhos de processamento de sinal em grafos.
Quando você aplica um filtro em uma foto para te deixar mais bonito você obviamente objetiva que as pessoas ainda te reconheçam. Isto é, as formas e aspectos mais importantes do seu rosto devem ser preservadas ou pouco alteradas. Vamos representar essas considerações por: $$ \begin{eqnarray} \mathcal P_{forma}(foto\ \ original) \sim \mathcal P_{forma}(foto\ \ filtrada)\newline \mathcal P_{cor}(foto\ \ original) \sim \mathcal P_{cor}(foto\ \ filtrada)\newline …etc \end{eqnarray} $$ Também espera-se que o ruído da câmera, rugas e imperfeições sejam reduzidas $\mathcal P_{rugas}(foto\ \ original) \neq \mathcal P_{rugas}(foto\ \ filtrada)$ e $|rugas\ \ foto \ \ filtrada|\ll|rugas\ \ foto \ \ original|. O símbolo $|.|$ significa que estamos contando o número de rugas da foto, do conjunto de rugas, e $\ll$ significa muito menor.
Da mesma maneira que no caso de fotos, se temos um grafo, $G$, queremos que sua versão filtrada, $\tilde G$, tenha uma ou mais propriedades (definido de antemão) preservadas após efetuar a filtragem, isto é $$ \mathcal P_{algo} (G) \sim \mathcal P_{algo} (\tilde G) $$
Sendo que o objetivo principal costuma ser uma redução drástica no número de relações (arestas), $|\tilde E| \le |E|$. OK, então antes de entrar nos métodos de filtragem precisamos discorrer sobre quais seriam essas propriedades que queremos preservar.
Diferente de uma imagem em que filtros só ocorrem nos valores definidos na posição dos pixels em um grafo, podemos filtrar tanto os valores definidos nos vértices/arestas quanto a própria estrutura do grafo em si.
- Novamente: filtrar a estrutura de um grafo $\neq$ filtrar valores definidos na estrutura de um grafo
Algumas propriedades de grafos
Componentes
Uma propriedade importante de um grafo é o número de componentes. Um grafo é fortemente conectado quando é possível sair de qualquer vértice e chegar em qualquer outro. Um grafo fortemente conectado tem apenas uma componente.
Por exemplo, abaixo é apresentado um grafo fortemente conectado
graph LR;
A---B;
D---A;
B---C
A---C;
D---E;
Ao remover a aresta $(D , A)$ obtemos o seguinte grafo
graph LR;
A---B;
B---C
A---C;
D---E;
Como é impossível sair de $D$ ou $E$ e chegar em $A$, $B$ ou $C$ após a remoção, o grafo não é mais fortemente conectado e tem duas componentes. Qual a relação disso com filtragem?
Para muitos problemas, espera-se que métodos de filtragem sejam bons em preservar o número de componentes. Pois isso afeta em muito as dinâmicas ocorrendo no grafo. Assim como algoritmos de análise de dados. x'
Imagina se ao realizar uma filtragem você remova uma aresta que impede a contaminação por um vírus entre duas cidades no seu modelo?
Comunidades
Dentro de cada componente de um grafo temos o conceito de comunidade. Intuitivamente, quando pensamos em comunidade no âmbito das relações pessoais imaginamos um grupo de pessoas que tem fortes relações entre si, muito mais fortes que as relações com outras pessoas fora do grupo. Por exemplo, família, colegas de trabalho etc. Nesse contexto, qual é a tarefa de detecção de comunidades? Como efetuar tal tarefa?
Suponha que você queira modelar o grupo de pessoas pertencentes a dois partidos políticos, opostos na ideologia. Você pode representar as relações entre as pessoas usando grafos. Colocando uma aresta entre uma pessoa e outra com o peso representado um grau de concordância entre certos assuntos. O que seria um algoritmo de detecção de comunidade em tal caso? Se temos o ground truth, isto é, o partido que cada pessoa se identifica, o algoritmo é uma função, $f$, que recebendo as relações , $E$, cospe um indíce que associa cada pessoa um partido $f: (Pessoa, E) \mapsto \{Esquerda,Direita\}$. Mas como construir essa $f$? Na minha opinião existem três caminhos principais:
Caminho 1: Inferir
- Pegue por exemplo a distribuição normal. Quando trabalhamos com dados que acreditamos que podem ser modelados por tal distribuição realizamos um processo de ajuste de parâmetros, tentando estimar a média e o desvio padrão da população. A ideia aqui é similar. Propõe-se um modelo capaz de gerar grafos tendo como restrições um conjunto de parâmetros.. O objetivo é otimizar tais parâmetros tal que o modelo generativo seja um bom candidato para gerador do grafo original.
O modelo generativo mais famoso é conhecido como Stocahastic Block Model (SBM). Em português, Modelo de Bloco Estocástico. Usando o networkx você pode gerar uma amostra de um grafo através desse modelo usando o seguinte código
import networkx as nx
import matplotlib.pyplot as plt
# esses são os parâmetros que definiram o número de indivíduos
# dentro de cada comunidade
n1, n2, n3 = 30, 40, 60
# esses são os parâmetros que definem a probabilidade
# de conexão entre indivíduos da mesma comunidade
p11, p22, p33 = 0.4, 0.3, 0.7
# esses são os parâmetros que definem a probabilidade
# de conexão entre indivíduos de comunidades distintas
p12 = .01
p13 = .1
p23 = .01
sizes = [n1, n2, n3]
probs = [[p11, p12, p13], [p12, p22, p23], [p13, p23, p33]]
g_sbm = nx.stochastic_block_model(sizes, probs, seed=0)
W = nx.adjacency_matrix(g_sbm).todense()
plt.imshow(W)
plt.show()

A ideia de inferência de métodos que usam SBM de forma geral é a seguinte:
- Extraia o conjunto de arestas, $E$, de um grafo qualquer: uma rede social, uma rede de transações financeiras, etc.
- Pegue um SBM, tente estimar o número de partições, probabilidade de conexões intra e entre grupos e em qual bloco cada vértice pertence tal que os grafos gerados pelo SBM melhor represente o seu grafo original. No final, você tem uma maneira de identificar com cada vértice uma comunidade (partição).
O SBM é poderoso e ao contrário dos outros métodos te fornece uma maneira de checar a qualidade das comunidades encontradas. Isto é, se fazem sentido ou só são frutos de algo aleatório. Contudo, por ser uma técnica mais recente com uma implementação difícil, não são todas as bibliotecas que fornecem esse recurso. A biblioteca mais famosa para SBM é o Graph Tool que consegue estimar comunidades para grafos com centenas de milhares de vértices. Não poderei discorrer mais ou mostrar como usar o SBM pois é um tema bem complexo, tema para um post separado. Mas o importante agora é você ter conseguido absorver pelo menos a ideia.
Caminho 2: Quantificar/Descrever
- Você parte de uma função $f$ qualquer. Exemplo, $f$ é uma função que identifica todo mundo como esquerda ou direita, um sorteio aleatório, etc.
- Com tal identificação você estipula uma grandeza que vai mensurar o quão forte é a coesão entre as pessoas de cada grupo e quão fraca é entre os grupos. Um exemplo de grandeza que mensura isso é a modularidade.
- Você irá alterar a sua $f$ tentando maximizar tal grandeza.
O networkx por exemplo possui um método de maximização de modularidade usando um algoritmo guloso. Vamos usar o grafo gerado pelo sbm para testar esse método usando o seguinte script:
from networkx.algorithms import community
def find_where(n, p):
return [i for i in range(len(p)) if n in p[i]][0]
def plot(g, community_index, p):
labels = [chr(ord('A') + i) for i in range(len(p))]
plt.scatter(range(len(g.nodes)), community_index)
plt.ylabel('Community')
plt.xlabel('Vertex Id')
plt.yticks(range(len(p)), labels)
plt.show()
p = community.greedy_modularity_communities(g_sbm)
g_sbm_community_index = [find_where(n, p) for n in g_sbm.nodes]
print(f"Found {len(set(g_sbm_community_index))} communities")
plot(g_sbm, g_sbm_community_index, p)
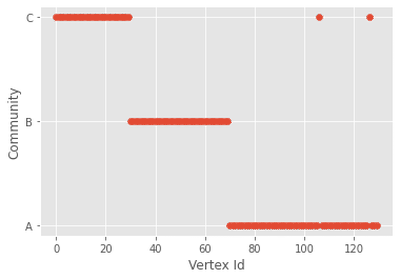
Temos um resultado muito bom. Mas será que podemos empregar isso em qualquer caso? Vejamos o que acontece quando aplicamos o mesmo algoritmo para um grafo aleatório.
# erdos_reyni é um modelo de grafo aleatório
g = nx.erdos_renyi_graph(150, 0.1, seed=0)
p = community.greedy_modularity_communities(g)
g_community_index = [find_where(n, p) for n in g.nodes]
plot(g, g_community_index, p)
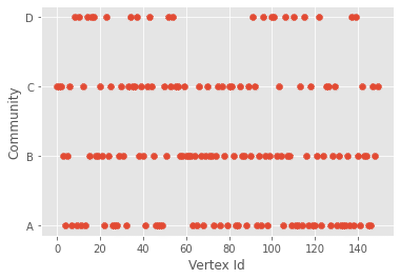
O algoritmo guloso encontrou 4 comunidades e o ponto ruim é que não temos como saber o quão confiável é essa resposta. Mas podemos dizer que provavelmente ela não deveria ser usada pois partimos de um modelo de grafo aleatório.
Devemos tomar muito cuidado com métodos de detecção por maximização de modularidade e similares. Recomendo ver alguns trabalhos sobre modelos de bloco estocástico, especialmente os feitos pelo Tiago Peixoto.
New blog post! This time, on something tame and uncontroversial:
— Tiago Peixoto (@tiagopeixoto) December 6, 2021
"Modularity maximization considered harmful"
It's the most popular method used for community detection. It is also one of the most problematic. 1/11
(Based on https://t.co/iCxFjKOIT1)https://t.co/IRdCFwttQL
Caminho 3: Visualizar
- Você utiliza um método que mapeia cada vértice do seu grafo em um espaço vetorial. Por exemplo t-sne, UMAP, force-directed, spectral embedding etc. Com sua visualização você realiza uma inspeção (totalmente subjetiva!) para identificar as comunidades (agrupamentos). Em alguns casos é aceitável realizar um k-means nesse espaço para encontrar os clusters.
O script abaixo gera uma visualização dos dois grafos usados nos exemplos anteriores: um obtido do SBM e outro do Erdos-Renyi.
import numpy as np
pos_sbm = np.array([ v for v in nx.layout.spring_layout(g_sbm, iterations=1000).values()])
pos = np.array([ v for v in nx.layout.spring_layout(g, iterations=1000).values()])
fig, (a1, a2) = plt.subplots(1, 2)
a1.scatter(pos_sbm[:, 0], pos_sbm[:, 1], c=g_sbm_community_index, cmap='tab20')
a2.scatter(pos[:, 0], pos[:, 1], c=g_community_index, cmap='tab20')
for ax in (a1, a2):
ax.set_yticklabels([])
ax.set_xticklabels([])
a1.set_title('SBM')
a2.set_title('ER')
plt.show()
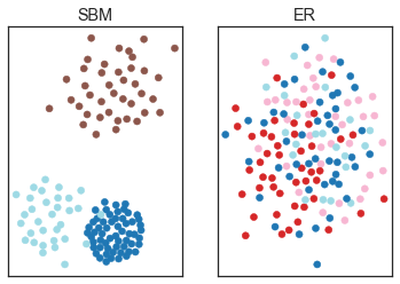
Note que o método de visualização mostrou um agrupamento de vértices para o SBM. Contudo, no caso do grafo aleatório (ER) só parece uma grande confusão. As cores representam as comunidades obtidas via maximização da modularidade. O que podemos tirar desse exemplo? Que você deve tomar cuidado quando falar que encontrou uma comunidade ou que existe uma “bolha” na rede social que você encontrou. Outra coisa que isso nos mostra é que usar métodos diferentes é uma boa alternativa para evitar ser enganado por seus resultados.
O tema de comunidades merece alguns posts separados para cada caminho, pois é um assunto denso e com muitos métodos diferentes.
Filtros
Estrutural: threshold
O método de threshold é um método estrutural, isto é, um método de filtragem que depende apenas dos pesos e das arestas. Com certeza, é o método mais simples e mais rápido, embora o mais controverso. É aplicável somente se cada relação (aresta) possuir um número real associado. O método de threshold consiste em descartar qualquer aresta cuja o peso ultrapasse um dado valor.
O método de threshold é muito utilizado em neurociência (com críticas) e para análise de dados em geral quando as arestas representam uma medida de correlação (Pearson) entre dois elementos. Como as medidas de correlações podem ser negativas é comum que o threshold seja aplicado no absoluto dos valores associados às arestas.
Tome o seguinte grafo como exemplo:
graph LR;
A-->|-0.5|B;
B-->|0.4|C
C-->|2|A;
D-->|-1|C;
Ao realizar um threshold de $0.5$ iremos remover a relação $(B, C)$ e $(A, B)$. O grafo não é mais fortemente conectado.
graph LR;
C-->|2|A;
D-->|-1|C;
B;
É comum que após o threshold todas as arestas que sobraram sejam truncadas em $1$. Ficaríamos com algo assim no final:
graph LR;
C-->|1|A;
D-->|1|C;
B;
Uma das maiores limitações/perigo de se usar o método um naive threshold é que em grafos que modelam situações do mundo real (seja ele direto ou não) a distribuição de pesos costuma seguir uma fat-tail e distorcida tal como essa aqui:
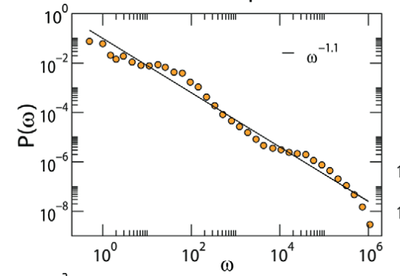
Bom, o que acontece se você tentar passar um threshold no grafo que tem uma distribuição parecida com essa na imagem? Vai ser difícil. Qualquer valor um pouco maior criará um monte de componentes desconectados. Além do que, como você justificaria seu valor de threshold ? Não dá para falar um argumento dois desvios padrões a partir da média. Se fosse uma distribuição normal de pesos você poderia estar bem.
O threshold tem outro problema, ele é local. Isto é, você poderia penalizar muito as arestas de uma comunidade e nada de outra. Para deixar isso mais claro veja o exemplo de grafo com pesos a seguir:
Se aplicássemos um threshold em $0.5$ teríamos algo do tipo
Produzindo 3 componentes no nosso grafo se alterássemos ligeiramente o threshold produziremos mais componentes ainda. Ele é muito sensível. Qual o problema disso? Se fossemos aplicar um algoritmo de detecção de comunidades teríamos que fazer isso para cada componente. Em uma rede social isso pode ser problemático porque já estaremos analisando “bolhas” isoladas. Então como proceder? Portanto, vocẽ pode até usar o threshold para encontrar as arestas que são a sustentação para o grafo. A espinha dorsal do grafo, backbone. Contudo, ele costuma falhar.
Pontos positivos
- custo computacional baixo $O(n)$
- apenas iterar e comparar os valores.
- paralelizável
- trivial de implementar
- apenas um parâmetro
Pontos negativos
- tendência de produzir muitas componentes desconectadas,
- parâmetro arbitrário,
- cherry-picking.
- A remoção de uma aresta só depende do valor atribuído a ela. Isto é, local.
Considerações finais
Outros métodos estruturais como o high-salience network tentam reduzir os problemas do threshold adicionando contribuições não locais. Isto é, uma aresta é mantida/removida dependendo também das outras arestas no grafo. Contudo, como o high-salience network É um filtro definido pelos menores caminhos no grafo ele costuma ser adequado apenas para grafos que esse conceito de filtragem é útil, por exemplo grafos que modelam infraestrutura de transporte.
Estatístico: quebrando a varinha, processo de Dirichlet
Métodos estatísticos têm uma abordagem mais generalista quando comparados aos estruturais. Pois métodos estatísticos não dependem de algum conceito direto como caminhos mínimos usados pelo high-salience network para redes de infraestrutura.
Um método estatístico muito usado para filtrar arestas faz uso do processo estocástico de Dirichlet. Intuitivamente, podemos usar esse processo para modelar uma situação que temos uma varinha e vamos quebrando ela em $k$ pedaços e queremos descobrir a probabilidade de um pedaço de tamanho $p$ aparecer no processo, stick-breaking process.
Certo, vamos tentar entender como usar esse processo para filtrar arestas.
Começamos definindo os pesos efetivos para cada vértice e aresta. Esse peso efetivo para uma aresta entre os vértices A e B é dado pela seguinte expressão: $$ p_{AB} = \frac{Peso\ da\ aresta\ (A,B)}{Soma\ dos\ pesos\ de\ todas\ as\ arestas\ de\ A} $$ $$ p_{AB}= \frac{w_{AB}}{\sum\limits_C w_{AC}} $$
Pegue o grafo a seguir com os pesos dados nas arestas
graph LR;
A---|1|B;
B---|1|C;
A---|2|C;
A---|4|D;
D---|1|C;
Calculando o peso efetivo para todas as arestas relacionadas ao vértice A. É fácil ver que
$p_{AB} =1/7$, $p_{AC}=2/7$, e $p_{AD}=4/7$ e claro que $\sum_B p_{AB}=1$.
graph LR;
A---|1/7|B;
B---C;
A---|2/7|C;
A---|4/7|D;
D---C;
Iremos decidir se removeremos alguma ou mais arestas de A.
Nossos pesos efetivos somam 1. A ideia do filtro é imaginar que os pesos efetivos são influências do vértice A nos seus vizinhos. O modelo parte da hipótese que os pesos efetivos são distribuídos de forma uniforme entres os vizinhos de A. Portanto, podemos modelar a distribuição de pesos nas três arestas de A como um stick-breaking process. Desta maneira, podemos escolher remover as arestas cujo os pesos efetivos tenham uma probabilidade maior de ter vindo desse processo. Estamos mantendo os pesos efetivos dispares do processo!
Ok, como fazer isso? Como os pesos efetivos podem ter qualquer valor entre 0 e 1 precisamos de uma densidade de probabilidade. O stick-breaking deve modelar um processo de quebra de um graveto em $k$ pedacinhos. No nosso caso, os $k$ pedacinhos são as $3$ arestas de A. Então a densidade de probabilidade precisa ter $k$ como parâmetro.

Demonstrar a densidade de probabilidade desse processo de quebra é trabalhoso, mas a expressão final é bem simples. São funções decrescentes que caem mais rápido quanto maior o $k$. O que faz sentido, já que quanto mais pedacinhos quebrarmos menos provável é achar um pedacinho com um tamanho próximo do original do graveto.
A filtragem via stick-breaking (disparidade) baseia-se então em remover somente as arestas cujo os pesos efetivos são mais prováveis (um p-teste) dado um fator $\alpha$ , um número real entre 0 e 1. Isto é, a aresta AB é mantida se a inequação abaixo é verificada: $$ (1-p_{AB})^{k_A-1} < \alpha $$
A tabela abaixo mostra o que acontece com as arestas de $A$ a medida que o parâmetro $\alpha$ é alterado
| Aresta/$\alpha$ | 0. 19 | 0.52 | 0.74 |
|---|---|---|---|
| A,B | Removida | Removida | Mantida |
| A,C | Removida | Mantida | Mantida |
| A,D | Mantida | Mantida | Mantida |
OK, parece muito bom. Mas veja o seguinte: ressaltei várias vezes A no texto. Isto por que o filtro é definido por vértice. Bom, e o que acontece se olharmos a partir do vértice B?
Partindo de $B$ teremos $p_{BC}=1/2$ e $p_{BA}=1/2$!
graph LR;
A---|1/2|B;
B---|1/2|C;
A---C;
A---D;
D---C;
Então $(1-p_{BA})^{k_b-1} = (1-1/2)^1 = 1/2$. Ok , então se escolhermos $\alpha$ igual 0.52 a tabela anterior (para A) diz para remover a aresta (A,B) enquanto por B o método nos diz que é para manter. Isso causa uma ambiguidade em como decidir se vamos manter ou não as arestas. Você pode escolher manter se os dois concordam ou manter se apenas um passar no teste. Essa ambiguidade não aparece no caso de grafos direcionados!
Pontos positivos
- é estabelecido dentro de uma formalização matemática robusta
- tenta evitar que o grafo se desconecte
- custo computacional baixo
Pontos negativos
-
podemos argumentar que o teste de hipótese é arbitrário
-
parâmetro $\alpha$ precisa ser escolhido, embora mais robusto do que apenas o parâmetro de threshold